Archeops Windows Functions v1

The data made available through this page has been updated. The most recent version of this data may be accessed through: Archeops 2005 Product Table

Download Links:

archeops_all_v1_get.html

These two files contain the window functions (in ASCII and FITS versions) for the Archeops power spectrum bins. The integral of the window functions are normalized to 1 for each of the 16 bins and are computed between l=0 and l=768. The table contains a float array with dimension 16 x 769 (16 columns by 769 rows). The window functions are defined as follows (with implicit sum over repeated indices):

$\begin{displaymath}\mathcal{C}_b=W_\ell^b \left[ \frac{\ell(\ell+1)}{2\pi}C_\ell \right]\end{displaymath}$

(1)

In the MASTER framework (Hivon et al., 2002), if we define $\mathcal{M}$ as

$\begin{displaymath}\mathcal{M}_{\ell^\prime \ell^{\prime\prime}}=M_{\ell^\prime......\prime\prime}}F_{\ell^{\prime\prime}}B_{\ell^{\prime\prime}}^2\end{displaymath}$

(2)

Then the window function reads:

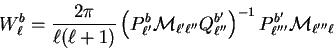
$\begin{displaymath}W_\ell^b=\frac{2\pi}{\ell(\ell+1)}\left(P^b_{\ell^\prime}\ma......rime\prime\prime}}\mathcal{M}_{\ell^{\prime\prime\prime} \ell}\end{displaymath}$